QPSK,16QAM信号の信号点間距離

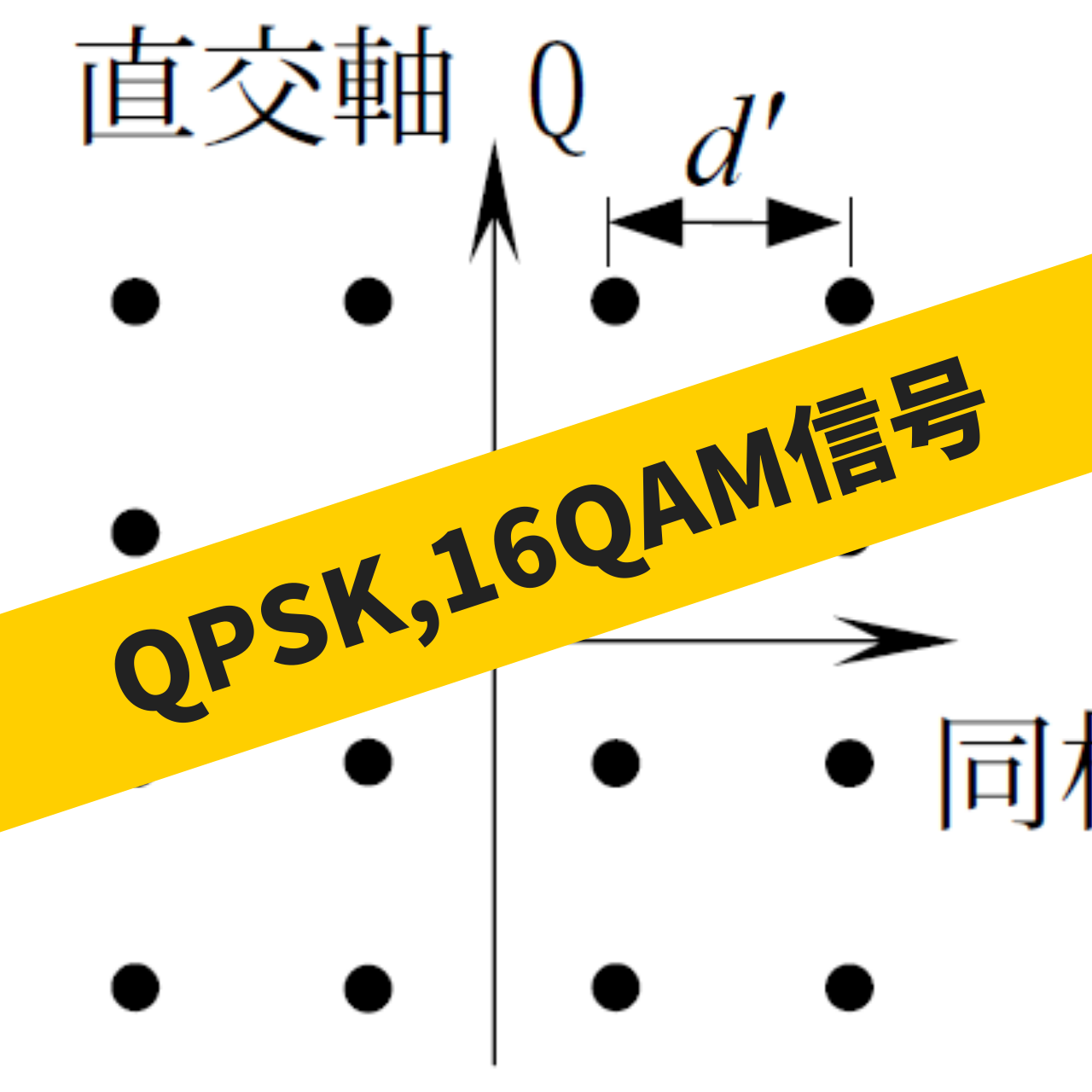
出典：第一級陸上無線技術士国家試験（平成30年1月）

デジタル変調に関する問題です。QPSK（Quadrature phase shift keying）は四位相偏移変調、16QAM（16-Quadrature Amplitude modulation）は直角位相振幅変調という変調方式です。
QPSKは4QAMとも呼ばれますので兄弟みたいなものだと思ってください。

問題を解く前に、直交軸Ｑと同窓軸Ｉで表される信号空間ダイアグラムが何を意味しているかを簡単に解説したいと思います。基本として知っておかなければならないのは位相変調と振幅変調という変調方法です。

まず位相変調と言うのは搬送波の位相を変化させることで信号を伝送する方式のことです。例えば問題にあるQPSKの場合は下の図のように90°ずつ位相が異なった4つの搬送波を使います。

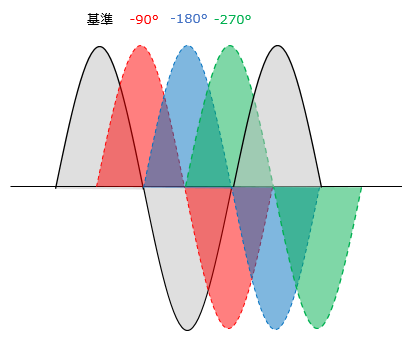
例えばそれぞれ異なった位相の送信波をそれぞれ「0」～「3」とし、位相を次々と変えることで、同じ周波数で４値の信号が送れます。

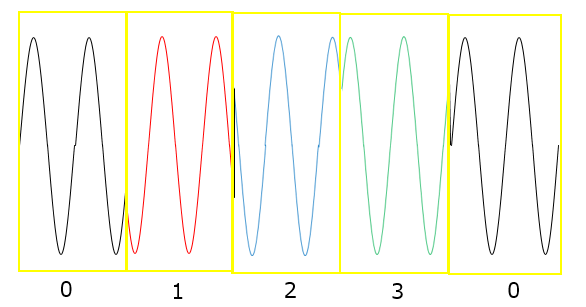
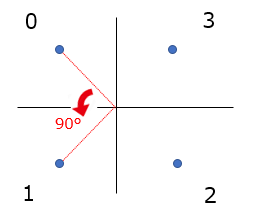
この０～３のデータを平面上に表したのが信号空間ダイアグラムでQPSKの場合はこのようになり、各信号同士の角度が位相を表しています。「０」と「１」は90°位相が違い、「０」と「２」は180°位相が異なることなどがわかります。

次に振幅変調ですが、これは搬送波の振幅を変化させて信号を伝送する方式です。このように信号の大きさ（振幅）によって信号を送ります。

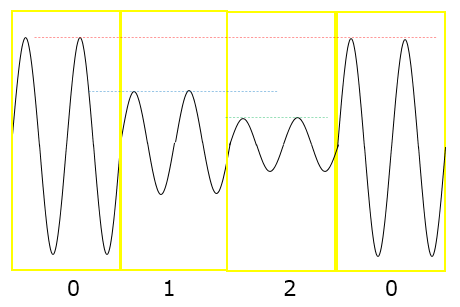
この振幅変調も信号空間ダイアグラムで表すことができます。先ほどのQPSKとは違い各データの位相は同じで、違いは振幅です。位相が同じなので「0」～「２」とも同じ角度上に位置し、振幅の違いは原点からの距離で表します。

では、16QAMとはどういう変調かというとこの位相変調と振幅変調を組み合わせた変調です。

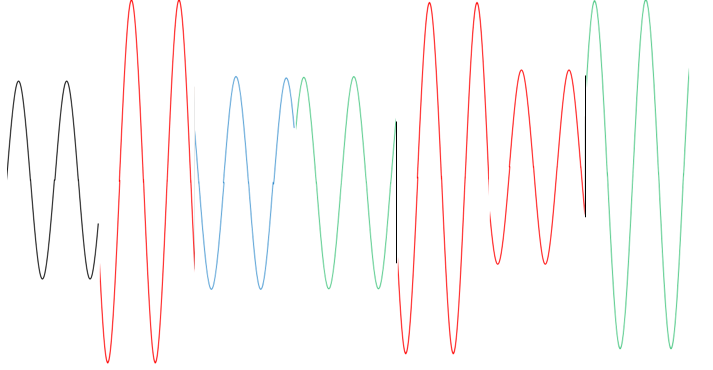
位相の変化と、振幅の変化を両方使うことでより多くのデータを送ることができます。

では実際に問題を解いていきましょう。
問題では信号空間ダイアグラムで原点からの距離は信号の振幅を表すという事だけ理解できていれば解くことができます。

（1）信号点間の距離がｄのときQPSKの最大振幅は「Ａ」で表せる
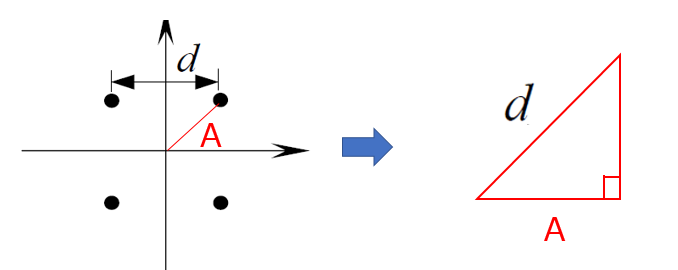
先ほど説明したように信号の最大振幅は原点からの距離です。QPSKは4つの信号がありますがどれも距離は一緒です。図のように最大振幅をAとすると直角二等辺三角形上に点が位置することがわかります。よって直角二等辺三角形の辺の比率からA：d＝1：√2の関係になることがわかり、A＝ｄ/√2が求まります。

（2）16QAMの信号点間距離をｄ’（ただしd’=d)としたき、 16QAMの最大振幅は「B」で表せる。
この問題も（1）とほとんど同じです。まず16QAMの最大振幅は原点から一番遠い所なので、最大振幅は４隅の点までの距離になります。

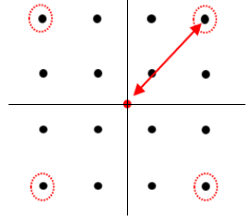
ここでも直角二等辺三角形なので各辺の比率は下図のようになることがわかります。

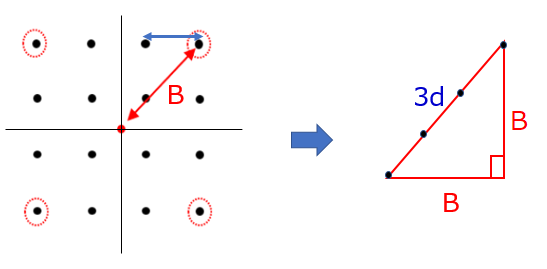
これより、Ｂ：3ｄ＝1：√2となり、Ｂ＝3ｄ/√2となります。

ここまで解ければ（3）を計算しなくても正解を選ぶことができますが一応見てみましょう。

（３）ｄとｄ’が等しい時、QPSKのピーク電力をｐとすると、16QAMのピーク電力は「Ｃ」である。
いままでピークの振幅について考えていましたが、この問題はピークの電力を聞かれています。無線信号の電力は波形を二乗平均して求めるため、（1）と（2）で求めたQPSKの最大振幅と16QAMの最大振幅を二乗します。

QPSKの電力　（ｄ/√2）²＝ｄ/2
16QAMの電力　（3ｄ/√2）²＝9ｄ/2

両方の電力を比較すると16QAMがQPSKの９倍であることがわかります。

答え「２」