出典:第一級陸上無線技術士国家試験(平成28年7月)
リサジュー図形に関する問題です。リサジュー図形とは、互いに直交する2つの正弦波を合成して得られる平面図形です。これは、2つの正弦波の振幅、位相、周波数の違いを視覚的に表現した図です。
位相が異なるような難しい波形は試験に出ないため簡単な解法がある!
オシロスコープの垂直入力と水平入力に異なる正弦波を入力することでリサジュー図形が得られますが、一陸技の試験で知っておくべき重要な事実があります。それは、2つの正弦波の位相が常に同じであることです。理由は、リサジュー図形から目視で位相の違いを判定することは、特定の条件を除いて非常に難しいからです。
この特定の条件と言うのは「位相が同じの時」でその時は必ず波形は(0,0)の原点を通ります。
原点を通らない場合の位相は大まかには判断可能ですが、目視で正確に知ることはできません。試験では明確に理解できる形で問題が出されるため、必ず原点を通る同位相の波形が使用されます。 したがって、同位相であることが大前提ということを理解した上で、問題を解いていきましょう。
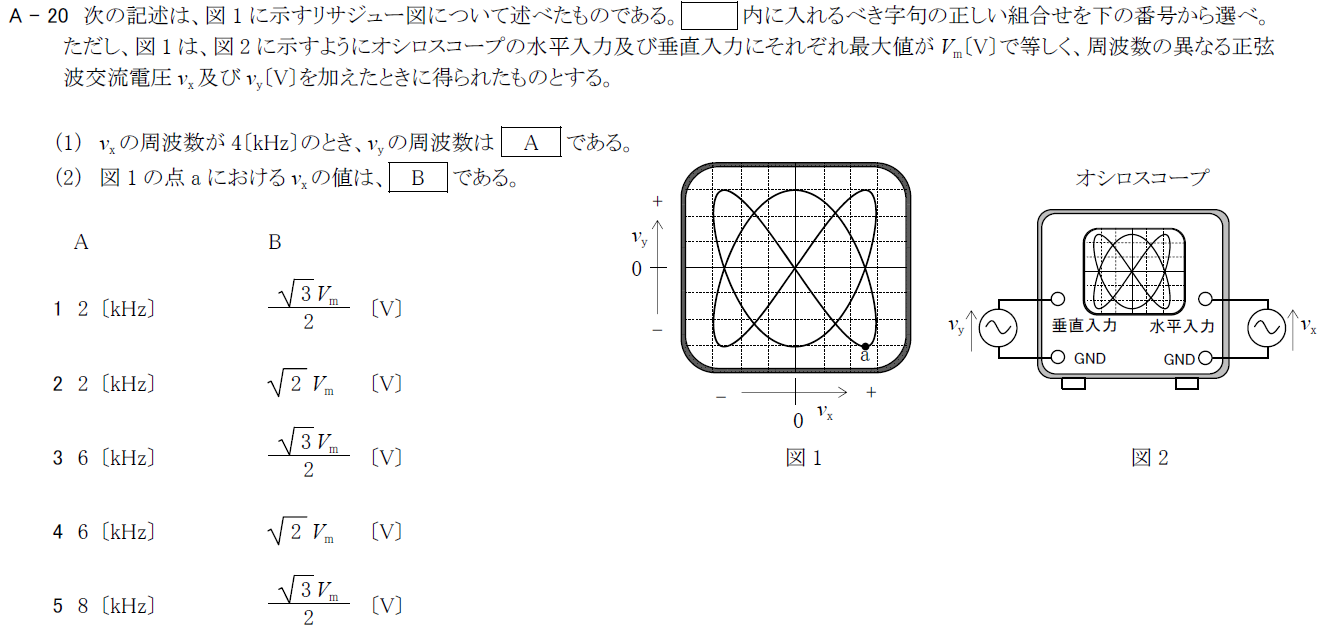
(1)vxの周波数が4[KHz]のとき、vyの周波数は( A )である。
リサジュー図形では周波数を直接知ることはできません。わかるのは2つの正弦波の周波数の比率なので、この比率の求め方を説明します。
まずvxの波形の周波数の求め方ですがリサジュー図形のvxが最大となるところに線を描きます。この線とリサジュー図形が接している点を数えます。この図形では2箇所で接しているのでvx=2とします。
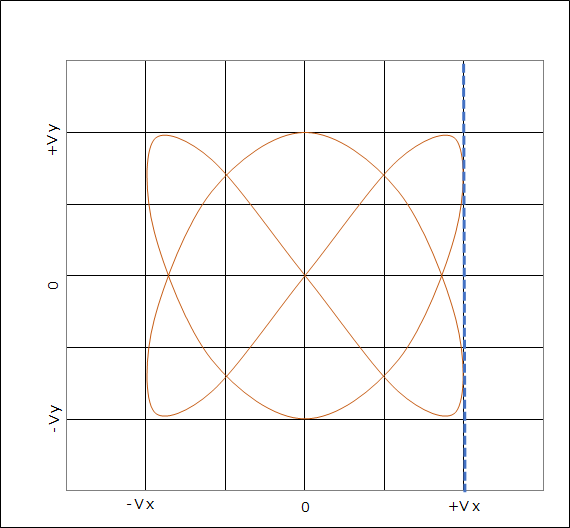
次にvyの周波数ですが、次はvyが最大になるところに線を描き同じようにリサジュー図形と接しているところを数えます。今度は3点なのでvy=3となります。
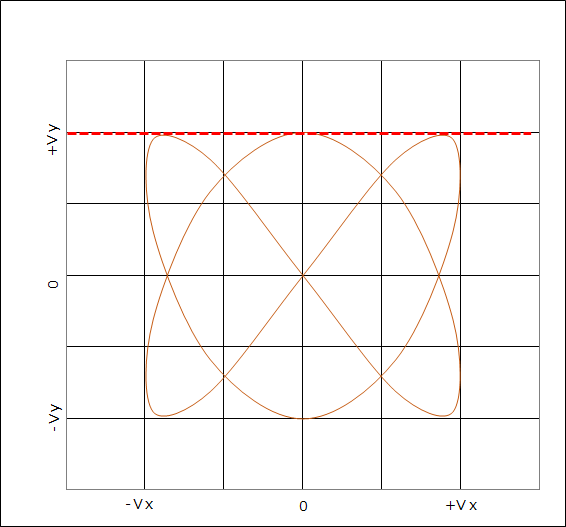
これがそのまま周波数の比率になるので vx=2、vy=3 より vx:vy=2:3で
vx=4[KHz]のときは vy=6[KHz] となります。
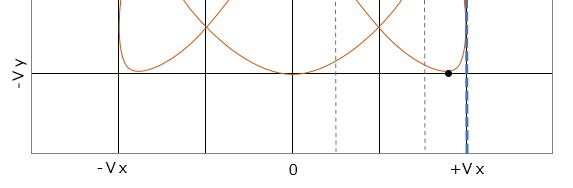
(2) 図1の点aにおけるvxの値は( B )である。
(2)の解き方はずばり目視です。+vxと0の位置がわかっているので点aのざっくりした値は図からわかります。点aは0.8~0.9vxくらいなのが目視でもわかります。(補助目盛を書くとわかりやすい)
選択肢をみてみると、√3/2・(vm) または √2・(vm)です。√3=1.73、√2=1.41なので計算してみると
- √3/2=0.865
- √2=1.41
先ほど目視で出した値とどちらが近いかと言うと一目瞭然ですね。というか√2は「1」を超えているので明らかにおかしいです。このように目視だけで答えは簡単にわかります。
周波数も最大値も見るだけで簡単にわかります
答え 「3」