直流ブリッジ回路による抵抗値

出典：第一級陸上無線技術士国家試験（平成30年7月）

直流電源が２つある回路で、負荷抵抗の消費電力を最大にする条件を求める問題です。
数値を変えて良く出題されるので確実に正解できるようにしておきたい問題です。

ただ、一発で答えのわかるような裏技がありませんので、正攻法で解いていきましょう！計算自体は難しくないので、覚えてしまえば大丈夫です。

この問題はノートンの定理を使って解いていきますが「ノートンの定理」ってなに？って方も多いと思いますのまずはそちらを説明していきます。

言葉だけだとちょっと何を言っているかわからないですね。図で説明しますと「線形に端子回路の短略電流I_s」というのは

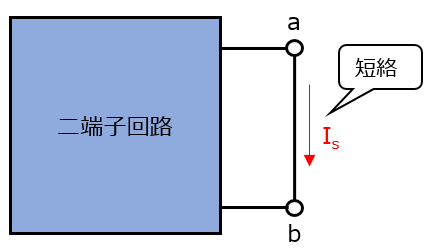
このように、ある回路を短絡したときに流れる電流のことです。
この問題では次のように考えます。

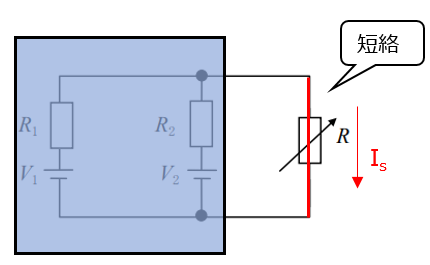
このときのI_sは、V₁とR₁の部分についてはV₁＝18V、R₁＝3Ωなのでオームの法則より18/3＝6[A]です。同じようにV₂とR₂の部分は12/6＝2[A]となり、Isはこの2つを足した電流なのでI_s＝6＋2＝8[A]となります。

次に「内部抵抗が R_i 」については同じ二端子回路で

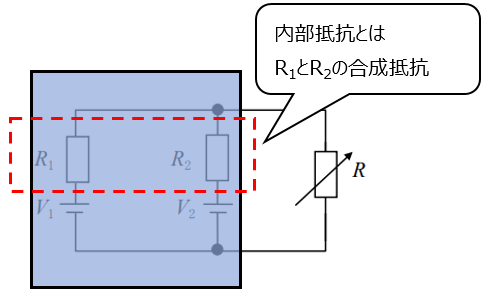
この図のようにR₁とR₂の合成抵抗の事を言います。
この2つの抵抗の合成抵抗はおなじみの並列抵抗の合成抵抗の公式

を用いて、Ri＝（3✕6）/（3＋6）＝2［Ω］となります

ここまで、I_s＝8A　Ri＝2Ω　を求めることができました。では、「I_s の電流源と抵抗R_i の並列回路と等価」というのは

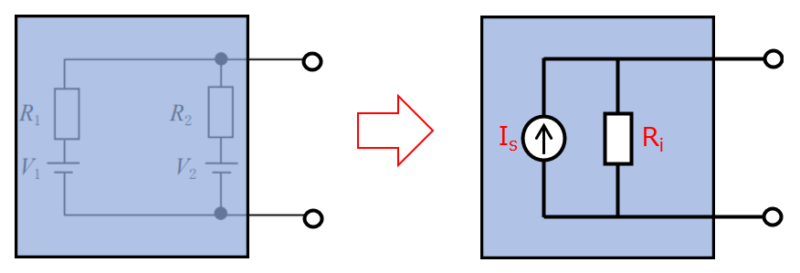
元の回路が右のように置き換えることができるということになります。ここまでがノートンの定理の説明になります。

ではこの置き換えた回路で問題に戻ってみると

電流源と抵抗2つのシンプルな回路になります。この時にRを可変させてRで消費する電力が最大となる条件というのは、R_i＝Rの時になります。これはインピーダンスマッチングと言われていますが、詳しく解説されているサイト様などがありますので、ここでは割愛しますが抵抗値が同じというところを覚えておいてください。

では実際にIs＝8A、R_i＝R＝2Ωとして計算すると、RiとRには同じ電流が流れるはずなのでそれぞれ4A流れます。この時にRで消費する電力は、I²R＝4²✕2＝32

答え「5」