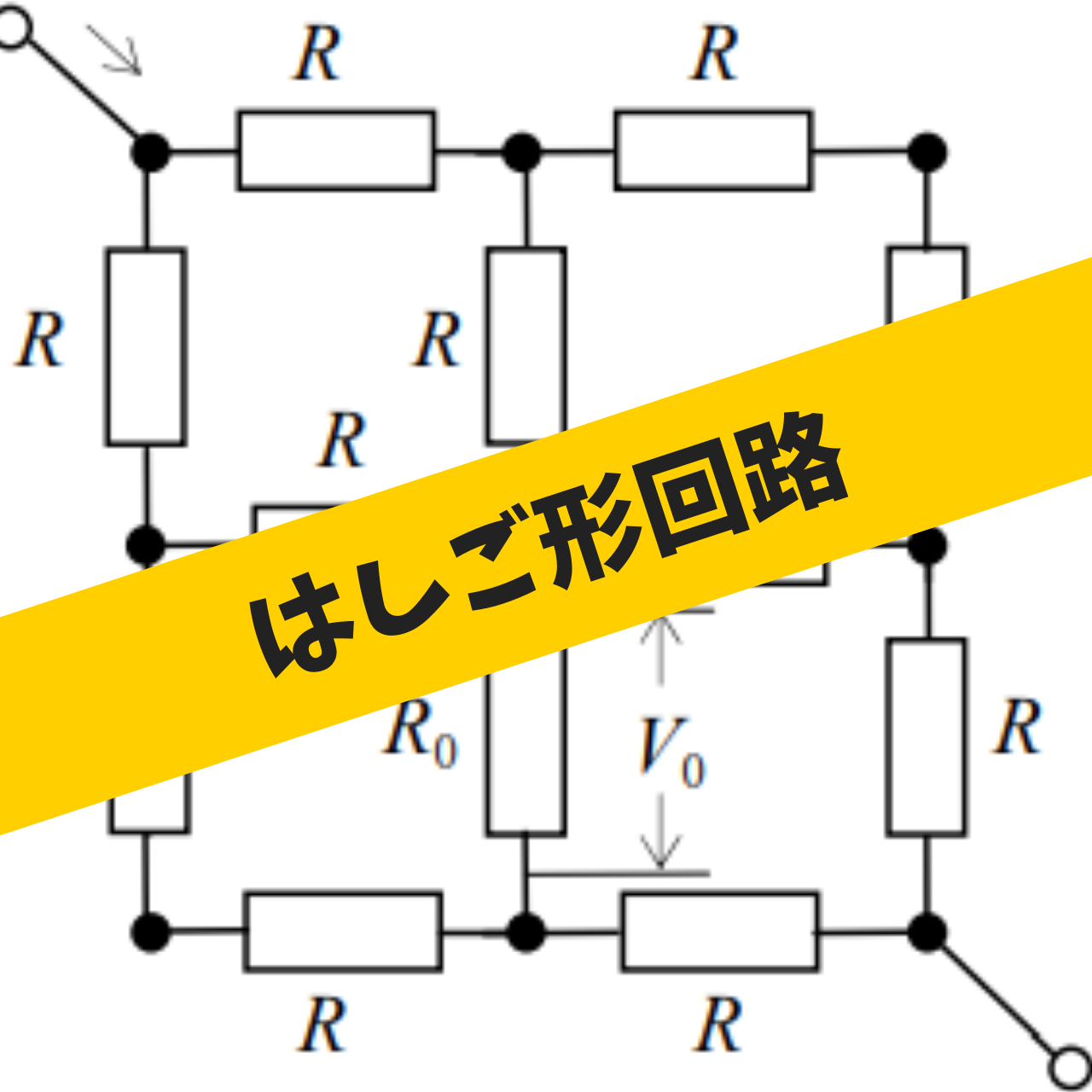
以前説明した、はしご形回路の合成抵抗の記事の補足説明になります。
前回開設したように計算でも解けますが、頻出問題についてはパターンを覚えてしまった方が早いのでそのパターンを紹介します。
良く出題される基本的な形は、以下の2つのパターンです。
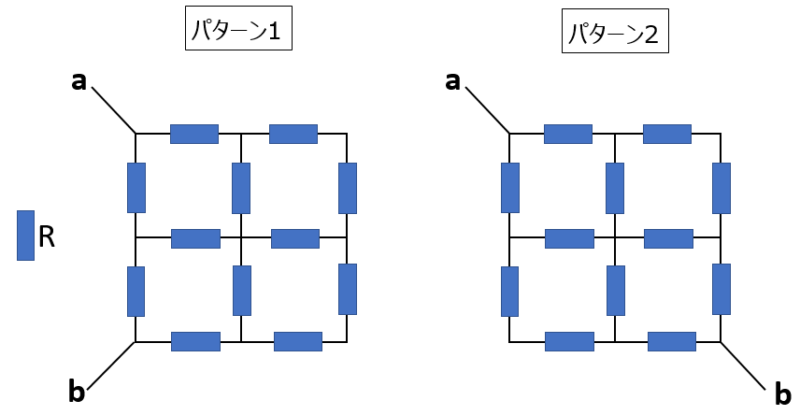
一つの抵抗をRとして、a-b間の合成抵抗がいくつになるか知っておくと簡単に問題を解くことができます。
合成抵抗のきまり
- パターン1の合成抵抗=1.25✕R
- パターン2の合成抵抗=1.5✕R
例えばR=20Ωとすると、次のようになります。
パターン1=(20✕1.25)=25Ω
パターン2=(20✕1.5)=30Ω
以前解説した問題を見てみると、これはパターン2をアレンジした問題であることがわかります。
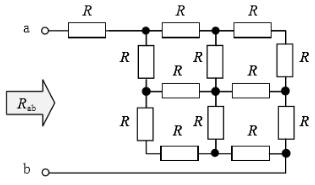
この問題ではR=30Ωなので、はしご形の部分は30✕1.5=45Ωです。それに直列に抵抗Rがついているので、30+45=75Ωと一瞬でわかります。
この2つのパターンは良く出るので合成抵抗が一瞬で分かるように覚えてしまうのが良いでしょう!