
出典:第一級陸上無線技術士国家試験(平成30年7月)
特性インピーダンスの問題です
特性インピーダンスを求める公式あり!
結論から言うと、無損失給電線のインピーダンスを求める公式があります
何も考えずにそれに当てはめるだけで大丈夫です

マイナス記号や「j」は無視して、開放時インピーダンス(90)と短絡時のインピーダンス(40)の数字部分を掛け算しましょう
90✕40=3600
そしてこれのルートをとれば答えになります
√3600 = 60
答えを簡単に導き出すことができますが、特性インピーダンスは非常に重要な概念ですので、少し詳しく解説します。特性インピーダンスとは、伝送線路を通過する交流信号の際、電圧と電流の比率が一定となる性質を指します。この一定の比率が特性インピーダンスです。
伝送線路は、下図に示すような等価インダクタンスと等価容量を持ち、これらの値を用いて特性インピーダンスZ0を計算できます。
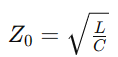
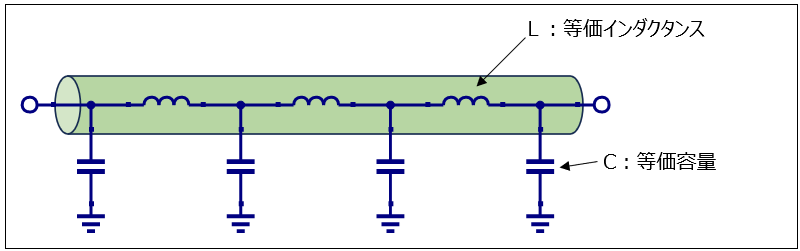
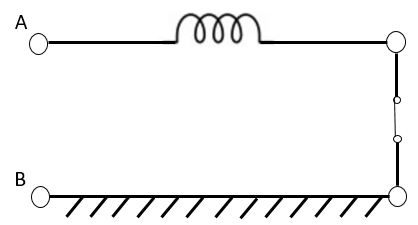
次に等価インダクタンスと等価容量をどのように求めるか見ていきましょう。問題文を再度確認すると、開放時のインピーダンスが -j90[Ω] であることが示されています。開放端とは、図のようにAからBへの経路が途中で開いている状態を指し、理想的な伝送路では電流は全く流れません。従って、理想的な開放端のインピーダンスは∞になるはずです。
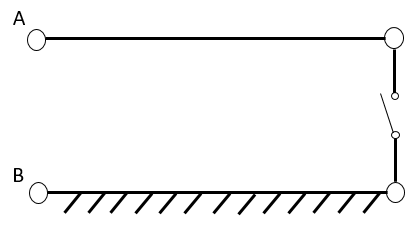
しかし、インピーダンスが -j90[Ω] であるということは、交流の状態では電気がある程度流れることを意味します。これは等価容量が存在し、このコンデンサのインピーダンスが 1/C = -j90[Ω] であることを示しています。
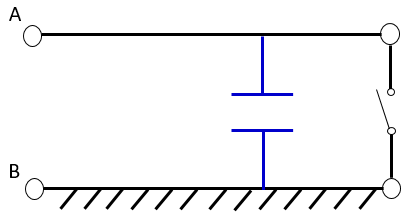
次に短絡端の状況を見ます。スイッチが閉じており、電流が自由に流れる(インピーダンスが0になる)状態ですが、短絡時のインピーダンスが +j40[Ω] となっています。これは等価インダクタンスが存在し、このインダクタンスの値が +j40[Ω] であることを示しています。

しかしながらこちらも短絡時のインピーダンスが+j40[Ω]となっています。これは今度は等価インダクタンスが見えるためです。この等価インダクタンスが+j40[Ω]ということを示しています。
ここまでで、以下のことが導き出せました以下の2つの値を
等価容量 1/C=-j90[Ω]
等価インダクタンス L=+j40[Ω]
先ほどの特性インピーダンスの公式(関係式①)に入れると答えが導き出せます。
公式で一発!

答え 2 ![]()


