円形コイルと直線導体に流れる電流が作る合成磁界

出典：第一級陸上無線技術士国家試験（平成27年1月）

円形コイルの中心における磁界の強さを求める問題です。円形コイルが発生する磁界と直線導線が発生する磁界の２つがありそれを合成する必要があります。

解法としてはビオ・サバールの法則から、円形コイルが発生する磁界と、直線導線が発生する磁界を求めてそれを合成することになります。

まず円形コイルに発生する磁界ですが、コイル状に電流Ｉが流れると図の矢印の方向に磁界が発生します。

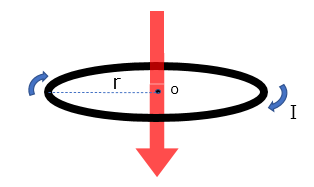
この時にコイルの半径をｒとすると、中心Ｏにおける磁界H_Aは次のようになります。

H_A＝Ｉ/2r [A/m]

次に、直線導体が発生する磁界は電流に対して右ねじの法則が成り立つので次の図のような円形な磁界が発生します。

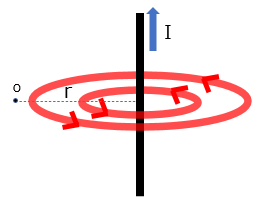
電流をπI、点Ｏまでの距離をｒとすると、点Oにおける磁界H_Bは次のようになります。

H_B＝Ｉ/2r [A/m]

そして、点OにおいてはH_AとH_Bは直交するので

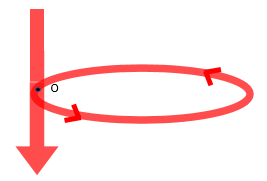
H_AとH_Bの合成磁界は三平方の定理で求めることができます。

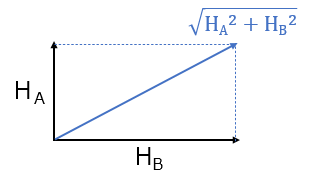
ちょっと長くなりましたが、ここまでが下準備でこれから問題の解き方を解説していきたいと思います。

まず、この「円形コイルと直線導体に流れる電流がつくる合成磁界」は良く出題されますが毎回全く同じ問題が出るわけではなく、一部の数字を変えて出題される「類似問題」です。ですので答えを丸暗記するので通用せず、問題の数字から答えを導き出す必要があります。

いま上で説明したのは以下の条件の場合です

• 円形コイルの電流：Ｉ
• 円形コイルの半径：ｒ
• 直線導体の電流：πＩ
• 直線導体と点Oの距離：ｒ

この場合はH_A、H_Bともに Ｉ/2r　になるので合成磁界は次のように表せます

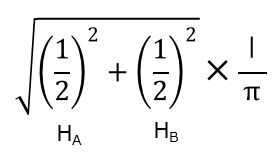
この式が基本になるので、ここまでは導けるようにしたいところです、覚えてしまっても良いですが。
過去に何度も類似問題が出ていますがH_Aの部分、つまりコイルに流れる電流Ｉやコイルの半径ｒは数字を変えられたことはないです。数字がいじられるのはH_Bの部分で、具体的には直線導体と点Oの距離ｒと直線導体に流れる電流πＩ、下の図で言うＡとＢの部分が問題により数字が変わります。

先ほどの式にあてはめると、このようになるのでＡとＢの部分を問題に合わせて数字を入れてください。

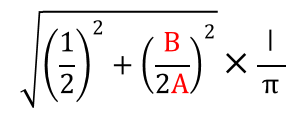
今回の問題ではＡ＝2、Ｂ＝1なので、その値を代入すると

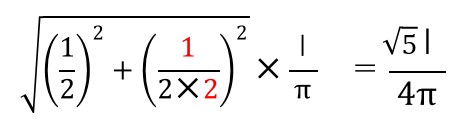
となります。

答え　「５」